What Is number system?
Number system is a technique to represent and work with number. Another definition of number system is, It is define a set of value that represent the magnitude of any quantity.
More know about octal number system click here
For more know about hexadecimal number system click here
Table of Contents
Importance of Number system
Numbers are basically used to count various items and number system is use to represent that numbers. In our daily life we use decimal number system for counting various items but electronics devices such as computer, digital watch does not understand decimal number system they understand and work on binary number system.
In a number the value of any digit can be determined by:
- By digit
- Its position
- Base of the number system
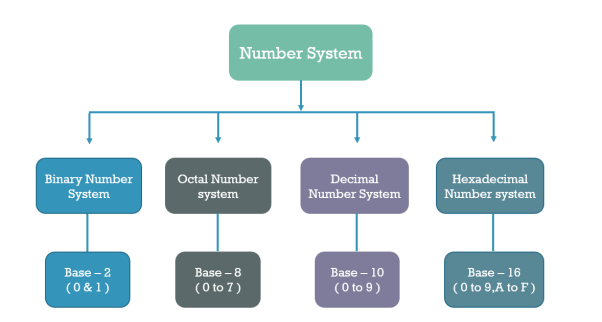
Types of Number system
There is various type of number system in which the four we commonly use
- Binary number system (Base – 2)
- Octal number system (Base – 8)
- Decimal number system (Base – 10)
- Hexadecimal number system (Base – 16)
Base of the number system is also called Radix and denoted by “r”. It define how many distinct digits in a number system.
We will discuss all these number systems one by one in detail
Binary Number System
The base (radix) of binary number system is 2 so it required only two different symbols 0 and 1 for its digits. Binary digit 0 and 1 is also called “bits” and bit is the smallest unit of data, 8 bits together make a byte. Computer stored and process data in the form of bits and bytes. Here 0’s and 1’s represents two voltage level 1 for high and 0 for low. The combination of bits 0 and 1 represent binary number for example: (1010)2, (1100)2, (10001)2.
Octal number
The base (radix) of octal number system is 8. So, it required eight different digits 0,1,2,3,4,5,6,7 to represent the octal number system. In the octal number system digits like 8 and 9 are not included. The advantage of octal number system is it has less number of digits compare to other number system so the chances of computational error is also less. For example: (345)8, (624)8 etc.
Decimal Number system
The base of decimal number system is 10. So, it required ten different digits 0,1,2,3,4,5,6,7,8,9 to represent the number system. It requires a dot to represent decimal fractions called decimal point. It is a weighted number system just like octal and binary number system each digit have a positional weight, that represent the different multiple of base. Decimal number system is very much important because it used in our daily life for various purpose like to count items etc. For example: (1659)10, (8627)10 etc.
Hexadecimal Number system
The base of decimal number system is 16. So, it required sixteen different digits 0,1,2,3,4,5,6,7,8,9, A,B,C,D,E,F to represent the hexadecimal number system. In hexadecimal number system each digit represents a decimal value, for example hexadecimal A is equivalent to decimal 10, hexadecimal D is equivalent to decimal 13 etc.
Q1. What is a number system?
A number system is a way of representing and expressing numbers. It consists of a set of symbols or digits and rules for their combination to represent quantities.
Q2. What are the commonly used number systems?
The commonly used number systems include the decimal system (base 10), binary system (base 2), octal system (base 8), and hexadecimal system (base 16). These systems differ in the number of symbols used and their positional value.
Q3. What is the decimal number system?
The decimal number system is the most widely used number system. It uses ten digits (0-9) and is based on powers of 10. Each digit’s position represents a power of 10, with the rightmost digit being the units place.
Q4. What is the binary number system?
The binary number system is a base 2 number system that uses only two digits: 0 and 1. It is widely used in digital electronics and computer systems, where information is represented using binary digits (bits).
Q5. What is the hexadecimal number system?
The hexadecimal number system is a base 16 number system that uses digits from 0 to 9 and letters A to F to represent values from 10 to 15. It is often used in computer programming, memory addressing, and representing binary data more concisely.
Q6. What is the octal number system?
The octal number system is a base 8 number system that uses digits from 0 to 7. It is commonly used in computer programming and represents groups of three binary digits (bits).
Wiki link